Rep-tiles, or how mathematicians start to puzzle and open up questions.
I thought it was time I did some actual mathematics here, and hope to attach it to some of my thoughts on how mathematicians ask questions. I will try to keep the presentation completely elementary, so the only prerequisite is a little interest. This is not intended to be a thorough survey with everything addressed, just a collection of opinions, you have been warned!
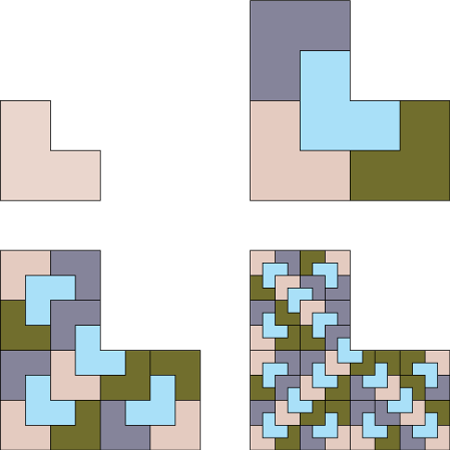
Let us start with an observation and a simple example. Take a L-shaped tile made of three squares, as shown below:
Keeping with this figure we find that that four copies of this tile make a larger version of the same shape. We can instead subdivide the tile, and this has the advantage of not making things larger and larger, two more subdivisions are shown in the figure. This process gives an interesting result. So where do we go from here?
The first thing is to choose a good name. To some mathematicians this is as important as the actual result. So these are tiles that replicate themselves. What can we call them? Rep-tiles of course. The danger of this name is that the joke has already been used by Escher. However I did not come up with it, I believe it was created for these tiles by Golomb, so will let it stand. Creating new names for things happens often and can be very confusing!
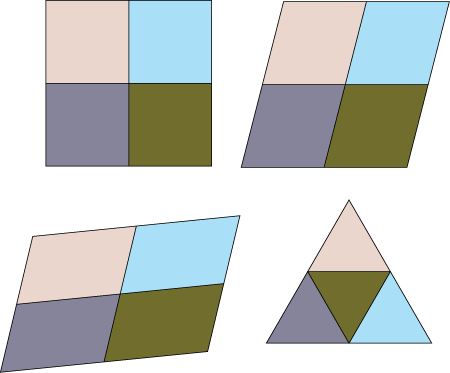
Now we have a name we can ask a first question. What shapes are rep-tiles? The first step is to find some more examples, both boring and interesting. Boring is nearly always easier (if it is not easy can it be boring?) so we see those first:
This raises an interesting question. Three of the rep-tiles above are in a sense the same. They are clearly different shapes, so they should be considered different rep-tiles, but we can change one into another in a simple way. So we can ask, what exactly do we mean by “the same”. This is something that mathematicians do a lot. We take some large set of objects and give some rules as which should be the same, we call them “equivalent”. For example here we say that the picture above contains only two different rep-tiles, not 4. Can you show why the chair rep-tile does not have any equivalent shapes?
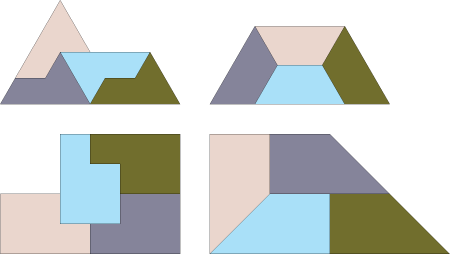
Returning to our quest, with a little work (and using the geometric intuition of many people) we find some more interesting examples:
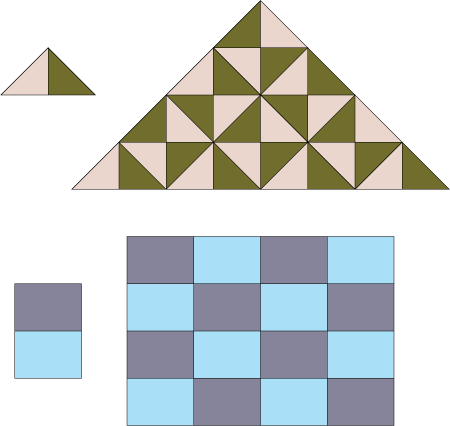
All the examples shown so far have one tile replaced by four. We therefore call them 4-reptiles. Are other numbers possible? As you can see from the first example, having a 4-reptile is also a 16-reptile (16=4×4) and a 64-reptile (64=4x4x4), by a similar argument all the examples so far are reptiles for any power of 4. Four is a natural number to use as it is the number of tiles we need to create a tile twice as large as the original. That is because we are doubling the lengths in the tile, so the area will increase by four. So let us consider what happens when we triple the lengths of the edges.
Here you see the chair tile as a 9-reptile. This obviously show us that it is also an 81-reptile, 729-reptile and so on. We can also combine the two rules to show that it is a 36-reptile as 36 = 4×9. So what other numbers are possible? Is the chair tile an n-reptile for all square numbers (4,9,16,25…)? The answer is yes, showing this does not require any complicated maths, though it does need some clear thinking. I encourage you to try and find at least some examples yourself. Alternatively you can find answers by looking at some of the reference websites I will put at the end.
We therefore have a first answer in our investigation, the square numbers can all have rep-tiles. That leaves a lot of numbers out! What about 2, are there any 2-reptiles? Again we start with some boring examples:
The second image here is related to the 4-reptiles for the square and others shown above. The division repeated twice again gives the same rule as described. Though I say this is a boring example, as the tiling produced can be produced by easier methods, it does one interesting feature. If you live outside the US you might use this shape every day and do so because it is a rep-tile! The A system of paper sizes A0, A1, A2, A3, A4… are based on this shape as two copies of each paper size makes the next size. Thus two sheets of A4 give a sheet of A3, two of A3 give one of A2, and so on.
To find more interesting examples of 2-reptiles we have to consider more exotic shapes. Here we start to go beyond the process of finding examples and start to ask the mathematical question of whether we can find every 2-reptile. In fact with some additional conditions, it has been proved that the image below, along with the boring reptiles above give all possible examples!

Interesting 2-reptiles, from the top left clockwise: Levy Dragon, Twindragon, Heighway dragon and Tame twindragon.
In keeping with the rep-tile theme these are called dragons. I do not know if this was originally deliberate. We now have a second answer, we have an idea of all possible 2-reptiles. If we come back to polygons, are there any n-reptiles, where n is not a square number and that I will not complain at saying they are boring? The answer is yes, and in fact there is an amazing tiling. It is a 5-reptile called the Conway-Radin Pinwheel tiling:
In all the examples above the tiles used in the tiling could be moved to each by translations and a finite number of different rotations. We could therefore consider a finite number of tiles and make the tiling with translations. That is not possible in this example, you can get a glimpse of this by looking at the second part of the picture where every tile is coloured by orientation. To get from one tile to every other tile in the tiling would require an infinite number of rotations. As the construction is so simple this a quite amazing fact (to me at least!).
Where does this leave us with rep-tiles? The initial question was to understand what was possible. We divided this problem up by considering the number of copies needed to make a rep-tile. For 2-reptiles we showed a complete list of possibilities. This leaves many open questions:
Are there n-reptiles for all whole numbers n? (maybe there is an answer to this, if you know please tell me)
Update (10/11/8):
Alon Levy of the carnival of mathematics and abstract nonsense, pointed out a simple construction of n-reptiles for any whole number n. It is shown below:
So we know that any n is possible. However without giving precise definitions I said above that certain rep-tiles were not interesting. I will stay away from defining interesting precisely here. However it leads me to mention the idea of definitions. At school mathematical definitions often seem to be the hardest facts imaginable. Few people would, for example, argue that numbers should be defined differently. Yet to find the definitions that mathematicians use for these things took most of human history. The definitions we use today for numbers and mathematics itself were first stated jut over 100 years ago. They are most clearly put forward in Zermelo–Fraenkel set theory. Finding correct definitions is therefore hard. In this case I considered rep-tiles and wanted to find interesting ones. I will still not make this precise (interesting for one thing can change, it can simply mean “truely different to known examples”), however I would say that the tilings generated by the rep-tile should be non-periodic. You might enjoy finding the following examples:
From the construction above can you give n-reptiles for any composite (non-prime) n that generate non-periodic tiling?
From the pinwheel construction can you find n-reptiles where n is the sum of two squares? (a construction also mentioned by Alon).
Finally a new general question for which I would love an answer. Can you find a general class of n-reptiles with more than 4 edges?
The chair tile is both a 4-reptile and a 9-reptile. What other numbers are compatible in this way? For example can a shape be a 2-reptile and a 3-reptile?
Several of the examples give above are shapes called polyominoes, shapes made by gluing squares together. What polyominoes can be rep-tiles?
The big question, can we gain a full understanding of rep-tiles in general? Maybe we can list all possible 2-reptiles and 3-reptiles, but 4-reptiles are too varied?
So to sum up, one approach to mathematical questions proceeds something like this. We first find something interesting. This opens a question and we try to find other examples with similar properties. We can then start to say which examples are really the same and which are different in some deeper sense. The final stage is to try to classify all possible examples. This is often too large a task, as was the case here, so we find ways that the problem can be divided up. This division can be to consider a subset of the problem, for example to consider polyominoes rather than all tiles, or to slice the problem into smaller pieces, for example to consider 2-reptiles and 3-reptiles rather than all possible rep-tiles. These partial results will often lead to new examples, and new ideas such as the change from polygons to fractal shapes. They may even show why the main problem is not possible to solve.
To find out more about rep-tiles search on the web, there is lots to find, but it can be a little hard as for some reason the biologists dominate the google results. Some good places are listed below, along with a couple of excellent books that consider rep-tiles along with a lot more interesting mathematics.
Rep-tiles references: Websites
http://www.meden.demon.co.uk/Fractals/reptiles.html
http://www.xs4all.nl/~wolter/index.html
http://www.geocities.com/alclarke0/PolyPages/RepO.htm
Rep-tiles references: Books
Martin Gardener The Colossal Book of Mathematics
Samuel Golomb Polyominoes: Puzzles, Patterns, Problems, and Packings: Puzzles, Patterns, Problems and Packings (Princeton Science Library)
One final note, this is intended to be an accessible mathematics piece, but it can be easy when talking about my own subject to lapse into jargon without realising it. If you have found some parts that are not easy to follow or confusing, therefore, please let me know.
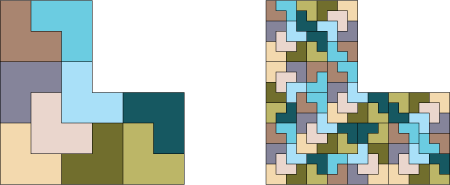



Fascinating approach! Beautiful pictures as well.
Pingback: Nerditudine allo stato puro
Pingback: The Math Factor Podcast » Harriss: First post
Very nice discussion, geleda. Any insights into why this general understanding of your big question, a classification of reptiles seems hard, even for polygonal tiles? (Especially for polygonal tiles?)
Heya, I’ve been searching in this topic for quite some time, and the pages I found seemed to talk about the same things over and over again. So I have a huge favor to ask: would you mind to email me some links you know ? I would be very grateful. My email address is minoriole@gmail.com
Thanks in advance!
Thomas
Pingback: Rep-tiles « MATH with my KIDS
Pingback: Tile Bathroom
Pingback: Escritor
Pingback: The 2×1 rectangle and Domes « Maxwell's Demon
Rep-tiles with holes:
what is are:
smallest number for no reflections allowed, not fractile
smallest number, reflections allowed, not fractile
ways to categorize rep-tiles with holes.
smallest odd number, non-fractile rep-tile with a hole
how can we categorize these?
Good questions!
ooxx
oxox
oxox
ooxx
a very simple rep-tile with a hole of size 16 made of squares.
You can of course cut out one layer and make it a 12 if you use rectangles (the ratio of the two sides
similar to what is described in the article: 90 degree rotation required).
ooxx
oxox
ooxx
right-angled triangles allow an 8 with a hole if reflections are allowed.
equilateral triangles allow an 81 (takes a bit of thinking about!).
Smallest odd one with a hole I can find…