Angle sum formulae
Only a short post this week. I am on holiday for a few days from tomorrow. Yippee!
In playing with algebraic equations I found myself wanting the angle sum formulae:
Being a forgetful sort I could only remember sketchy details and in particular certainly could not remember which was round the equation for goes. So I decided to construct them for myself, and found they both come from the same elegant picture. Maybe this is well known, but I do not remember ever proving these equations, so I do not know the standard proof. Looking for geometric proofs I found several, going back all the way to Euclid, even the Wikipedia proof is geometric. However:
[these] geometric arguments (while they lend themselves to spiffy pictures) tend to involve a certain amount of chicanery. One must find the proper “construction lines,” inscribe and circumscribe the correct circles and so forth. If one sees a geometric proof and, six months later, wishes to recover the result, remembering the necessary diagrams and manipulations can be quite the challenge.
Blake Stacey Science after Sunclipse
The other method (used by Blake in his post) is to step into analytic geometry and use Euler’s formula, however I feel that this construction is elegant and easily memorable, plus it does both formulas at once.
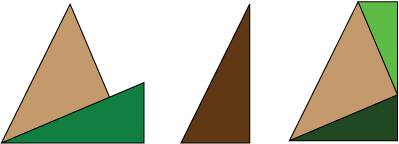
The angles of the light brown and green triangles sum to give the angle of the dark brown triangle. Adding similar green triangles (dark and light) to the light brown triangles gives the angle sum formulae.
If we have a right angle triangle with hypotenuse of length 1, and angle then the adjacent side next to the angle is
and the opposite side, away from the angle is
. In the figure therefore let the green triangle have angle
and the light brown triangle have angle
. Adding these two angles gives the angle for the dark brown triangle. We want to find the two side lengths of this triangle. To do this leave the light brown triangle fixed and stick two copies of the green triangle to its opposite and adjacent sides. These are of different sizes but are similar to the green triangle, so they have the same angles. In particular the dark green triangle is
times the green and the light green is
times the green. We can now read off the formulae. For example, the height of the dark brown triangle is the sum of the opposite side for the dark green and the adjacent for the light green.

Very nice!
Just recently, Kristen Fouss, @Fouss on twitter, posted a few tweets (1 and 2) to help remember the formulas:
sinbad luvs cosette, sits by her on dbl date (sin(u+v)=sinucosv + cosusinv), cosette doesn’t luv sinbad, makes him sit in back . . . . . cos(u+v)=cosucosv-sinusinv.
I’m lazy, so what I do is remember the formula for sin(a+b), and then differentiate it to obtain the formula for cos(a+b). I also remember that sin(-a) = -sin(a) but that cos(a) = cos(-a).
Those are easier to remember as I use them more often, and they are obvious from drawing a circle.