Prime Phyllotaxis Spirals
The phyllotaxis spiral is one of the classical forms of mathematics, and there is a wonderland of resources available online both images and explanations. The basic idea is to put points round in a spiral with the same angle between each point. This gives a family of forms:
Note that, as the angle changes the dots sometimes pack in better than others, this can actually be studied and the best packing is related to the golden ratio. The points in this spiral are placed down in order, so we can associate each to a whole number:
Now when I see a lit of numbers like this, I want to pull out the primes, see what pattern they make:
There are some hints at patterns, lets expand out, and look just at dots:
There seem to be spiral arms which are richer in prime numbers than others. We can analyse things further by colouring each number depending on its prime factors. The more prime factors the lighter the number, giving the image for the start of this post:
Now there is a clear pattern, light and dark arms spiraling out. Can we understand this pattern?
Think about the construction of a phyllotaxis pattern we turn the same angle every time, that means within a particular pattern we can find other phyllotaxis patterns. The one at twice the speed, three times the speed and so on. For example we could dive our pattern into two patterns each with twice the rotation angle. This gives:
All prime number (other than 2) are odd, so they must lie on the subspiral corresponding to the odd numbers. In addition it turns out that the spiral arms that we see are related to the Fibonacci numbers (themselves closely linked to the Golden Ratio). The particular curves we see relate to 144. Here is the spiral given by multiples of 144, pulling out just one such curve:
Note that in the prime factor picture this curve gives a very light line as every number in it is a multiple of 144, and 144 itself has 6 prime factors (three twice and two four times). Taking the multiples of 6 instead of 144 (which gives us several of these curves as 6 divides 144) we see another pattern of lines that are light in the image:
More importantly the curves next to these ones give numbers one more or less than a multiple of six. Every prime number has this form (all other numbers are multiples of 2 or 3 or both). This gives the curves of prime numbers we saw.
So by considering the construction of the initial image it begins to reveal its secrets. Yet, just as with the primes on their own there seems to be plenty of mystery left for investigation…


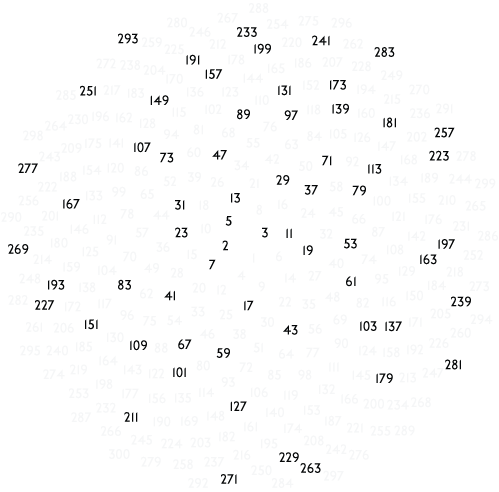






Kewl.
KEWL!!!!!!!!!!!!!!!!!!!! 😀
i agree 🙂
@Makdooda Liltha
Yes, very cool.
I wrote a paper on colouring this spiral, not with prime numbers but with the number of terms in the Zeckendorf representation of each integer. This also has some really cool patterns: http://www.ms.unimelb.edu.au/~segerman/papers/sunflower_spiral_fibonacci_metric.pdf (was published in the Bridges conference proceedings 2010)
Lovely work, Henry, the fundamental pattern is so compelling it is great fun to add patterns on top.
I’m reminded of the “rose” animation pattern pioneered by John Whitney – http://en.wikipedia.org/wiki/John_Whitney_(animator) – I recently worked with some colleagues to produce a collection of realtime animations based on Whitney’s work. This is one of them: https://vimeo.com/38744162
Pingback: Non-linear Pattern Web Quest « mboyer819
Pingback: Non-Linear Pattern Web Quest | mathwithmrswendling
Pingback: mathematics | Annotary
Pingback: Non-Linear Pattern WebQuest | Math and Technology
Pingback: Non-Linear Pattern Web Quest | crazyaboutmsmath
Here’s a Phyllotaxis generator:
http://www.interactive-earth.com/pattern/
I’m just starting my high school research on this topic but in connection to pine cones. I would be really grateful if someone told me about a programme where you’ve done the plotting of the numbers and points. and if anyone feels like explaining some extra questions to me, I would really appreciate it.
I used the general purpose math software Mathematica. If you can do some programming there is a free alternative called SAGE, that is worth looking in to.
very interesting page. I’m writing about something I have not seen tried before: regarding your vimeo video called “Phyllotaxis spirals” *and* the 2nd, 3rd and 4th picture below the video, which are phyllotaxis spirals with only the primes showing – if you were to rotate those prime spirals in those pictures, in exactly the same way as the fully populated spiral is rotated in the video, would that not be something brand new? I haven’t seen that done anywhere. I’m conjecturing that unprecedented prime patterns may just show up there. it would be sort of like a Ulam spiral but vastly superior, because instead of having hard 90-degree jumps like the Ulam spiral does, you’d have a completely smooth phyllotaxis spiral, rotating while showing only the primes. just like in your video, how things line up at the square root of 2, square root of 3, etc., primes might unexpectedly line up in unforeseen ways in the scenario I described.