Rational parameterisation of the circle


I really like parametric functions. You take two functions from the reals to the reals and use them to define x and y coordinates of points. For example you can take

f(t)=(\sin(a t), \cos(b t))

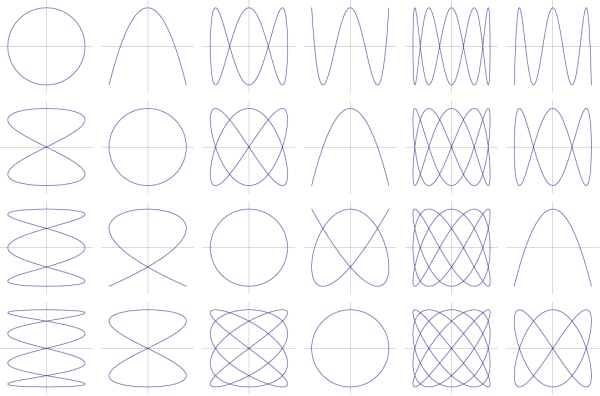
and you get the Lissajous curves:

Lissajous

These are a generalisation of the circle, that appears when a and b both have the same value, or simply for the function

c(t)=(\sin(t),\cos(t)).

Now consider another parametric function:

c'(t)=(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}).

Set x=\frac{1-t^2}{1+t^2} and y=\frac{2t}{1+t^2}, this means that

x^2 + y^2 = \frac{(1-t^2)^2 + (2t)^2}{(1+t^2)^2}

which is:

\frac{1-2t^2+t^4 + 4t^2}{(1+t^2)^2} = \frac{1+2t^2+t^4}{1+2t^2+t^4} = 1

So the parametric function satisfies the definition of the circle x^2 + y^2 = 1, which surprised me as I did not think that the circle had a parameterisation by such rational functions (one polynomial divided by another). In fact the lack of such a function was the source of questions and proofs on math.stackexachange.

So why do we go through all the trouble of creating sin and cos (ok they do have other uses!). One reason comes when we look in more detail at each parameterisation. When you just look at the points given by the function you ignore how fast those points change position as t changes. If we space points out equally by t we get the following images:

Circle_param

With c(t) (on the left) we get the points equally spaced around the curve, but c'(t) needs to use the whole real line with changes in t moving the point less and less as t increases. You can analyse this in more detail by looking at the differential of the parametric function. In fact that is how I sized the circles in the image.

There are also some interesting connections between the parameterisation c'(t) and the function arctan (think differential).

The fact that none of this makes the proofs on math.stackexachange incorrect is left as an exercise!

I can’t leave without showing the Lissajous curves with their dots. You can also explore these patterns for your own parametric functions.

Lissajous_dots

Category : General