The TMC Logo

February 9, 2014

Collegiate typography parsed into a fractal, with the theme of lots of parts coming together to make the whole.

That’s the corporate design spin on the new logo for the Twitter Math Camp, but for an audience of mathematics geeks a little more detail might be appreciated. So here goes.

The image of the logo uses a technique to visualise functions from the plane to the plane. We are familiar with visualising functions from one dimension to one dimension. This can be done with a line plot, the y axis value of a point giving the value of the function at that point, for example $f(x)=\sin(x)$ :

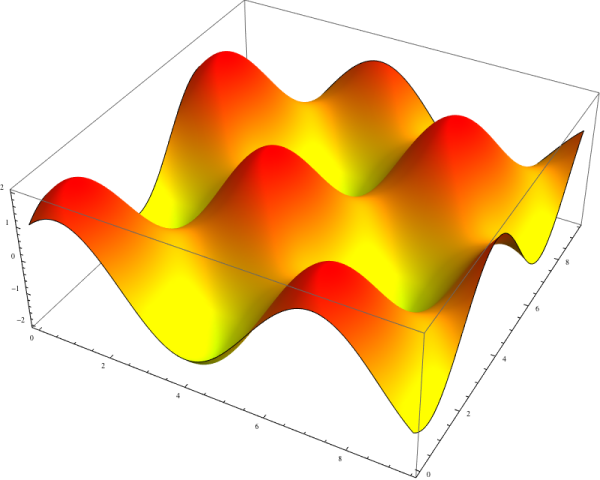
You should go and play with this in desmos. Functions from two dimensions to one dimension, for example $f(x,y)=\sin(x+y)+\cos(x-y)$ can be shown using three dimensions. In this case we look over a range of possible values of x and y and create a surface where the height is given by the value of the function.

Here we hit a snag. Our eyes and brains have never been trained to see beyond the three dimensions our reality provides. This is really quite unfortunate, as a lot of mathematics only really starts to get going in three or four dimensions. Luckily space is not the only dimensional thing we can perceive. There is also colour. We can redraw the previous image colouring by height, from yellow at the bottom to red at the top:

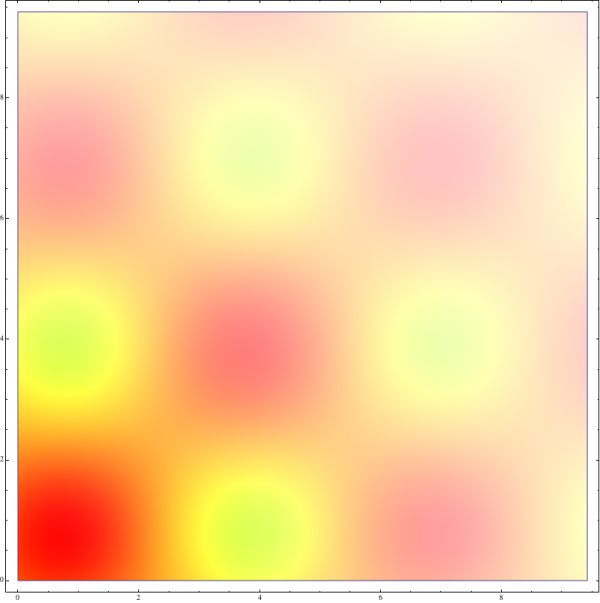
Now the information is in the colour we can remove the height, just showing a flat image with the function determining the colour at a point:

We can now take advantage of the dimensions of colour for example a second function can leave the colour the same but make it lighter. So we can use a new function that takes in two numbers and gives two numbers back $f(x,y)=(\sin(x+y)+\cos(x-y), \frac{30}{x^2+y^2+30})$ the first number gives the colour as above, the second lets the colour fade with the function creating a fade as we go further from the bottom left corner:

So we have solved our problem, by using two spacial dimensions and two colour dimensions we can visualise functions that take in two number and give two numbers out. In fact we can go further as our perception of colour is a three dimensional system, with independent amounts of red, green and blue. These actually do not model colour at all, as in the world each wavelength of light is independent so colour is infinite dimensional. Our eyes, however, only have three sorts of receptors so the infinite dimensional space is projected onto a 3 dimensional one. It is quite possible to have higher dimensional perception of colour with more receptors. Most birds and some fish and turtles have been found to have four channels of colour perception, leading to an experience of colour far richer than we can imagine (but still far short of reality).

Just dealing with two dimensions though does turn out to be incredibly powerful, thanks to complex numbers, which make many mathematical problems easier and are used throughout science and engineering. They can be expressed as two dimensional numbers over the real numbers we have been using so far, through the Argand plane. So a function that takes a complex number to another complex number is 2d to 2d (over the real numbers) and is precisely the situation we have described. The process of visualise complex functions in this way is called domain colouring, and I have linked to a google image search, though be prepared for intense psychdelia (in the name of math). To explore the topic in more detail the book Visual Complex Functions by Elias Wegert is beautiful and worth getting just for the images.

To get to the TMC logo, we have to leave behind using the dimensions of colour, however, and use a different method to colour our image. We are dealing with a function that takes in two (real) numbers and gives two (real) numbers back. We can use the two numbers we get out to find a point on the plane, a point in an image, and use the colour of that image at that point. The result is called the pullback of the image through the function, as we can consider that the image has been literally pulled back through the function.

For the logo I started with a pattern made up of the letters TMC: then made the letters fade out as they went away from the centre:with the image in place I could start to explore complex functions through this notion of pullback. Generating huge worlds of potential logos:

For these images, however, the letters TMC are hard to pull out. A better candidate is $f(z) = -z(z+1)(z-1)$ :The final image used this, though breaking the purity a little the three middle copies of the letters were removed to be replaced with an undistorted version. Of course you can also switch the image, I hope Megan does not mind me using her copy of the iconic image from TMC13 pulled back through $f(z) = i z(z^2-i)$ : As a final note you might notice that the final logo has a different colour to all the examples shown here. Just as colour can be generated from numbers we can also pull numbers out of a colour, change them and then go back to colour, in this case shifting red to blue.